比特币是否需要担心量子计算机?
在当下的计算机硬件条件下,“RSA公钥加密”以及“椭圆曲率加密算法”这两种加密方式是比特币及其他加密货币比较常用的,也是绝对安全的。
这里的“安全”并不是指无法破解,而是指破解的代价很大,需要投入极大的算力成本以及运算时间,所以可以认为是“无法完成”的任务。
就拿RSA来说,它的暴力破解涉及到一个很大很大数字的质因数分解。它的算法复杂度是指数级的。比如拿下面这个数字来说:
(图片来源:油管)
目前我们用的计算机需要2000年的时间才能完成它的质因数分解!所以没人会傻到花这个时间去破解。
很遗憾的是,它的破解难度只是在目前的计算机硬件环境下成立,但是在不久的将来也许会有一种叫做量子计算机的玩意儿可以打破这个算力僵局,在几秒钟内就能轻松地完成破解任务。到那时候比特币以及其他各类加密货币必然会沦陷。所以现在有不少业内人士忌惮于量子计算机的威胁,提前开始布局抗量子加密算法,准备应用于加密货币中。
而要了解抗量子加密,我们首先要搞明白量子计算机是怎么一回事。所以我们今天就来谈一谈这个话题。
什么是量子?
要了解量子计算机,首先我们要搞清楚量子是什么东西,有哪些特征?我们知道自然界的物质都是由分子构成的,而你将分子继续分割下去就会获得原子。每个原子又由质子,中子和电子这些微小粒子组成。我们把这些微小粒子统称为量子。
如何理解量子这个玩意儿呢?你可以把量子看成是一个很小很小的球,和你平时玩的篮球一样,它可以在空间中自由移动,旋转。只不过它的运动方式和篮球有点不一样,因为它并不遵循牛顿的经典力学。所以像加速度,动量,惯性这些理论在量子世界里并不适用,它有自己的一套运动规则,科学家称之为量子力学。
同样是球,量子的运动规律和你平时玩的篮球会有哪些不一样呢?我们来看以下这个实验:
(图片来源:油管)
如上图所示,我们从远处向一块幕布(猫的位置下面)发射一个个皮球。但是中间有一堵墙恰好有两个缝隙,皮球可以从缝隙中穿过。如果皮球穿过后撞到幕布,我们就在触碰的位置描红。越红的地方说明皮球从这个位置穿过的概率越高。随着时间推移,幕布会呈现以下的图案:
(图片来源:油管)
这个很好理解。因为皮球若能碰到幕布,那只有从缝隙处过,而弹射到边上的概率比较小,所以靠近缝隙处的位置肯定是最红的。
假设现在我们把球缩得很小很小,墙的缝隙也变得很窄很窄。实验结果竟会变得完全不一样!如下图所示:
(图片来源:油管)
我们可以看到幕布上的红带已经开始向两边扩散,最终演变成下面的图案:
(图片来源:油管)
这就是量子的运动轨迹。我们可以看见幕布上已经没有了像之前那样两条非常粗的深红色竖纹,取而代之的是多条分散的深红色竖纹。这也说明了同一个量子在同一个时间可以处在不同的位置。
而科学家发现只有一种现象才能解释幕布上的图案,那就是波!
(图片来源:油管)
由于量子波的特性,使得它可以在同时间处在不同位置,我们称之为量子态。另外根据幕布上条纹的深度,我们还可以发现不同量子态的概率分布也不尽相同。虽然同个量子可以有不同量子态,但是我们在观测的一刻只会随机呈现一种状态。
其实一开始的皮球也有波的特性,只不过由于它的质量比较大所以波的能量就比较集中,就会呈现出以下形式:
(图片来源:油管)
所以理论上你的爱人也可以在同时间处于不同位置。但是你每次观测的时候她都是在同一个地方,是因为她的质量足够大,所以产生的能量波比较集中,使得她出现在同一个位置的概率是100%!
为什么会有量子计算机?
如我之前所说,量子可以同时出现在不同位置,每个位置都对应不同的量子态,呈现不同的概率分布。事实上除了空间信息以外,量子本身的旋转方向也是一种量子态。它可以同时出现正旋和反旋,两种状态有各自的概率。也就是说你上一秒观测到一个质子是正旋,下一秒的观测也有可能是反旋。
为了便于计算,我们通常用|0⟩来表示反旋状态的量子,用|1⟩来表示正旋状态的量子。而我们知道一个量子可以同时有正旋和反旋两种状态,所以我们也可以用向量 
小于1的情况就是量子纠缠。说明有另外一个量子与其相互耦合,整个概率分布是由两个量子来决定的。但是我们今天讨论的量子计算机不会涉及到量子纠缠的情况,所以我们可以认为两者概率之和为1。于是就有:
有人可能会好奇为什么α和β是复数?那是因为量子有波的特征,而波除了幅值(amplitude)以外,还有相位(phase)信息。但是没有关系,为了方便起见,我们接下来的计算尽量会用实数进行。
所以根据向量表示法,我们也可以把|0⟩写成以下形式:
这个很好理解。因为|0⟩是反旋的量子,所以它反旋的概率必然是1,当然也就有α=1,β=0。同理,我们也可以得到:
所以对于更加通用的情况来说,任意一个量子态|ϕ⟩都可以表达成:|ϕ⟩=α|0⟩+β|1⟩
这也说明了任意量子态之间可以进行线性叠加,并且叠加后的状态同样也是合理的。
量子的叠加性是量子力学的一个重要特性,它奠定了量子计算机的理论基础。
除了叠加性以外,线性也是量子力学的一个重要特性。这个性质非常美妙,因为它可以让我们之后所有的计算变得异常简单。比如说z = 2x + 3y ,那U(z) 就可以写成2U(x) + 3U(y) ,其中U可以是任意的函数。
很多人认为量子力学是一个很高深的学问,但你们慢慢会发现它的计算其实比经典力学容易很多。牛顿的经典力学其实是非线性的,比如加速度的计算,它会涉及到平方的运算。如此一来你就不能进行简单的线性拆分。
我们再回过头来看量子,我们知道单个量子可以表示成向量
假设有两个量子位,|x⟩与|y⟩,其中:
则两者的张量积为:
所以如果两个量子都是反旋,那它们的量子态就可以表示为:
类似的,我们也可以得到:
根据量子的线性叠加原理,我们还可以把这些量子态通通累加起来,获得一个新的量子态,也同样是合理的:
由此可见,如果我们有两个量子位,就可以用来表示4个不同的信息位。
3个量子的情况也可以用类似的方法演算,获得8个不同的信息位。依次类推,如果是n个量子的话,就可以表达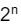
量子门电路
我们知道经典计算机都是由门电路所构成,量子计算机也不例外。
所以要搞定量子计算机,首先就要做出可以作用于量子位的门电路。幸运的是,我们已有的数字门电路的逻辑和机制对于量子位也同样适用。所以在制作量子门电路的时候,许多常用的数字门电路都可以照搬过来。唯一不一样的一点是,对于量子门电路的逻辑必须是可逆的,不可逆的门电路是无法实现的。
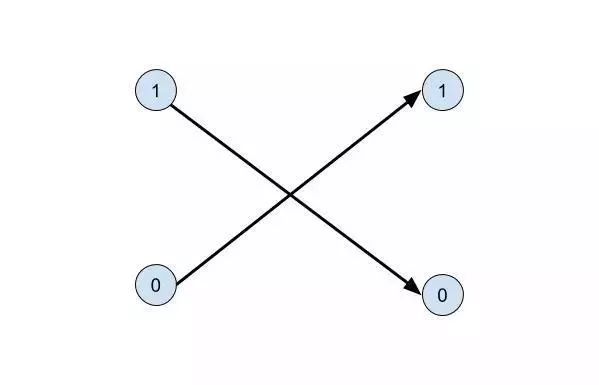
判断门电路是否可逆主要看能否通过输出把输入给反推出来,这个性质和函数的可逆性是一样的。举个例子,非门就是可逆的。因为f(x) = ~x,所以输出就是输入的取反。
如果我们知道输出是1的话,那就可以推出输入为0,反之亦然。它的门电路矩阵就是:
而异或门(XOR)就是不可逆的,因为我们通过真值表可以看到输出(Out)并没法反推出输入X与Y。如下所示:
在以上真值表中,如果OUT=0时,X与Y的组合有两种情况:(1,1)或者(0,0),所以无法确定输入到底是什么。由此判定异或门不可逆。
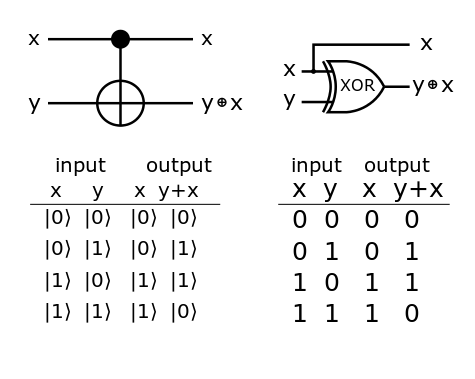
但是XOR毕竟是门电路中最重要的一种,因为它是构成加法器的基本元件。如果忽略了它,就没有计算机。所以为了引入量子版的XOR,我们必须做一些小的改进。最好的办法就是引入一个控制位来操控输出,并且输出增加到两个,如下所示:
其中x就是控制位,当它为0的时候,输出和输入保持一致,而如果它为1,则y值取反。这样一来就能保证输入与输出是一一对应的,从而使得门电路的逻辑是可逆的。由于控制位的出现,这个改良版的门电路被称为Controlled-Not,简称CNOT。CNOT是量子计算机中比较常见的门电路。它的门电路矩阵如下:
还有一个在量子计算机中比较常用的电路,也是量子计算机独有的,叫做哈达玛门电路(Hadamard gate)。它的作用就是可以将一个|1⟩或者|0⟩的量子位转化成两种状态的等概率叠加。它的门电路矩阵如下:
我们可以看到|0⟩通过哈达玛矩阵变成了|1⟩与|0⟩的叠加,并且两者的概率都是0.5。这个门电路非常有用,尤其是在傅立叶变换中,我接下来会仔细讲。很多经典的量子计算机算法都少不了它。
破解RSA的量子算法
介绍了完了量子门电路,我相信各位对量子计算机应该有诸多幻想。正所谓幻想无数,不如动次真格。我们现在就来动真格,看看用现有的工具能不能解决一些实际问题。我们回到文章最开始的世纪难题,有没有一种快速有效的算法来进行质因数分解?
答案是肯定的。这个算法的名字叫Shor,因为发明者叫Peter Shor。我们先来看这个算法是怎么一回事?
假设我们要对整数N进行质因数分解,它的具体步骤如下:
1. 任意选择一个随机整数a
2. 计算a与N的最大公约数gcd(a,N)
3. 如果gcd(a,N)=1,那我们可以直接返回结果
4. 反之,我们要就要找出函数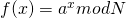
5. 如果r为奇数,或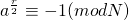
6. 反之,我们可以计算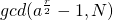
大多数人第一次看到这个算法会比较懵圈。没关系,我会帮大家理清思路。
简单地来说,此法的精髓就是猜数字,猜一个和N有公约数的数字。因为最大公约数的求法非常简单,用欧几里得算法几步就可以完成,求得的结果自然就可以被N整除,质因数分解也就完成了。所以问题的关键就是如何以最快的方法猜出这个数字?
我们先瞎蒙一个数字a,如果a恰好和N有公约数(当然这个概率极小),那自然就搞定了。如果这个数不对,那我们再猜一个数字r,但是这次可不是瞎蒙,而是更高级的猜法。因为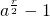
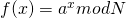
但是这里有两个疑点:1.为什么r一定存在?2.为什么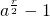
先来解释第一个疑点。r的存在性可以简单地通过欧拉定理来证明。
根据欧拉定理,如果a与N互质,则存在r=ϕ(N)使得ar ≡ 1 (mod N) 。其中r=ϕ(N)就是欧拉函数,它是所有小于N并且与N互质的整数的个数。比如说N=9,那就有1,2,4,5,7,8总共6个数与N互质,所以(9)=6。
(欧拉定理其实就是费马小定理的扩展,证明也是类似的。)
由于ar ≡ 1 (mod N) ,根据同余性质我们在两边乘上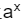
而我们知道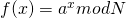
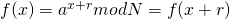
再来看第二个疑点。我们可以通过反证法来证明。
假设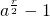
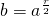
b ≢ 1 (mod N) (1)
并且根据算法第5步,我们也可以得到:
b ≢ -1 (mod N) (2)
由于gcd(b-1, N)=1,根据贝祖定理,必然存在整数u,v使得:
(b-1)u + Nv = 1 (3)
等式两边同时乘b+1,可以得到:
(b2 - 1)u + Nv(b+1) = b+1
可是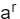
b2 -1=(b+1)(b-1) mod N=0
而根据(1),我们知道b-1无法被N整除,所以只能是(b+1) mod N = 0,而它又与(2)矛盾。所以我们可以证明gcd(b−1,N) ≠ 1 ,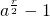
虽然两个疑点都解释清楚了,我们知道要找到r使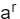
别急,你可别忘了f(x) = f(x+r),这也就说明f(x)是一个周期函数!对于一个周期函数来说,把它的时域信息转换成频域上的信息,是傅立叶变换的拿手好戏。而量子计算机牛逼之处,就可以用一步计算把所有可能的输入通通叠加在一起,通过傅立叶变换的特征,把干扰项相互抵消,只留下周期信息。接下来我就来跟大家详细介绍这个过程。
量子傅立叶变换
没有学过信号处理的童鞋们可能会对傅立叶变化比较陌生。简单的来说傅立叶变换的作用就是把函数的频谱和相位信息解析出来。
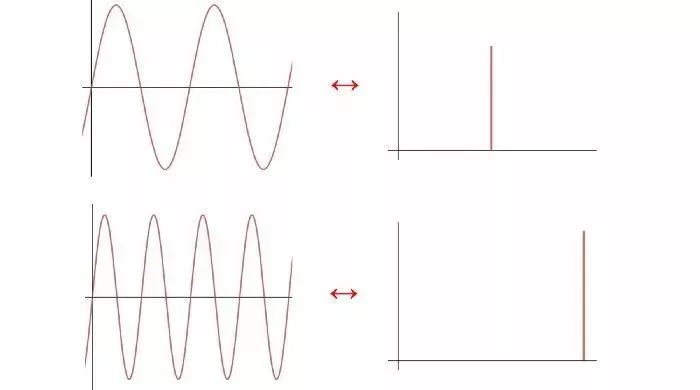
举个很简单的例子,f(x) = sinx。它的周期为2,频率是1Hz,幅度为1,所以我们在1Hz的位置画一条高为1的竖线,就是它的频谱。而如果f(x) = sin2x,它的频率就是2Hz了,所以就在2Hz的位置画竖线,如下所示:
(图片来源:medium)
左半部就是sinx和sin2x时域上的图形,而右半部就是它们对应的频谱信息。类似地,我们还可以根据频谱把它在时域上的函数还原出来,这个过程叫傅立叶逆变换。
(图1,来源:medium)
当然我们还可以把不同频率的sin和cos函数都叠加起来,会构成新的波形。它对应的频谱也会把这些正弦函数的频率都表示出来。
(图片来源:维基百科)
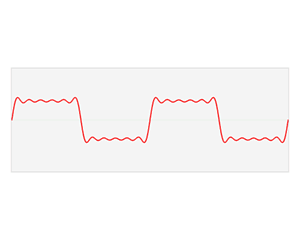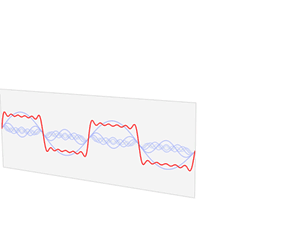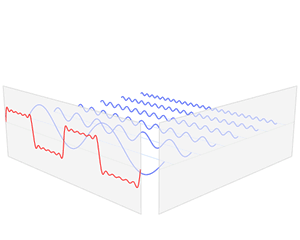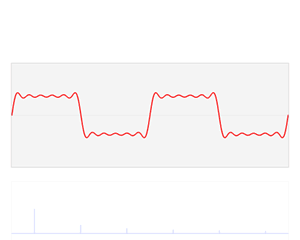
如上图,我们可以看到那个带锯齿的方波是由不同频率和幅度的正弦函数所叠加而成。这些正弦函数也被我们称为谐波。
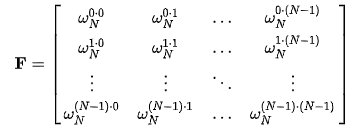
傅立叶变换有连续和离散之分,如果时域上的函数是连续的,那就需要用连续傅立叶变换来分解它的频域。比如上面我用的例子就是连续傅立叶变换,但如果是离散函数,那就需要用离散傅立叶变换(Discrete Fourier Transform)来做,简称DFT。由于我们观测到的每一个量子态都是离散的,所以量子傅立叶变换本质上就是DFT。我们可以把离散函数看成是连续函数的采样,所以在DFT的计算中,需要先定义一个采样频率N,也就是在一个周期内采样N个点。
对于DFT的计算,可以通过以下公式来进行:
其中k就是频域上的横坐标,n为时域上的横坐标。N就是我上面说的采样频率。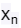
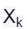
除此之外我们还可以看到等式中有“i”的存在。这就说明它的结果是复数,包含谐波的相位信息。因为对于一个正弦函数来说,它可以发生位移。比如sinx向左平移4个单位就变成了sin(x+4),虽然它们的频率和幅度都是一样的,但相位是不一样的
虽然有复数的情况会显得很复杂,但大家不要慌,因为对于量子傅立叶变换来说,它的相位信息并不重要,我们最关心的是它的频率信息。
除了DFT以外,它还有对应的逆变换IDFT,两者几乎是一样,只是符号和系数不一样,如下所示:
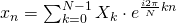
如果我们把等式右边拆开来就是:
而其中
就是方程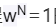
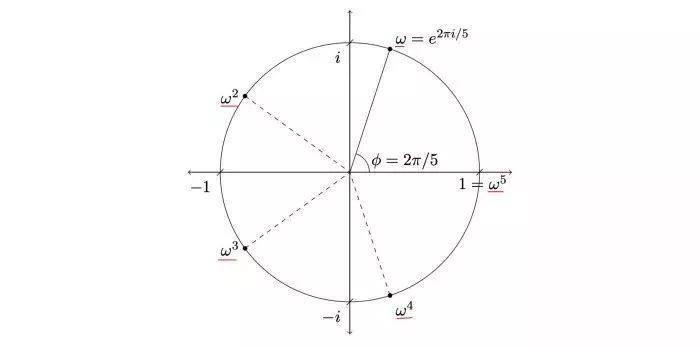
如果N=5,我们把w画在复数平面上就是:
(图片来源:courses.edx.org)
当然公式(5)代表的是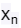
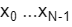
其中
为了运算标准化,通常需要在前面乘上系数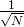
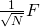
举个例子,如果我们对量子态|10⟩进行IDFT,我们可以运用DFT矩阵来进行变换。由于是两个量子位,一共有(|00⟩,|01⟩,|10⟩,|11⟩)四种不同组合,所以我们取N=4:
对于上面的结果,我们来分析一下它的物理意义。
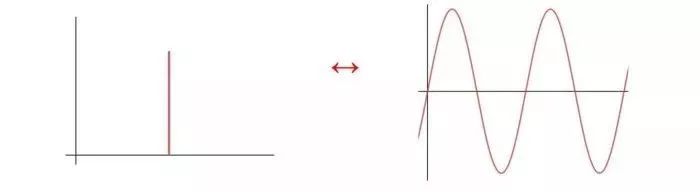
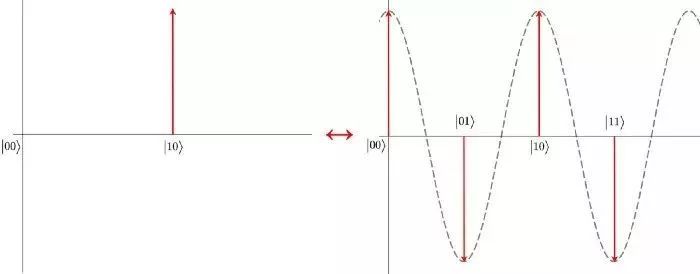
如果把|10⟩在时域上画出来,其实就是横坐标2上的一个脉冲信号,相当于频域上只有2Hz这一个点。所以它的傅立叶逆变换应该是一个和图1类似的正弦曲线,那它的离散形式就应是正弦信号的采样,如下所示:
(图片来源:medium)
而我们知道量子有叠加性,所以最终会以一个叠加的形式呈现:
那我们来看一个更加通用的情况。假设我们的输入是不同量子态的线性叠加,那经过量子傅立叶变换,它的输出也是不同量子态的线性叠加,如下所示:
以上就是量子傅立叶变换,简称QFT。和公式相比,我们可以发现它和IDFT并没有什么太大区别,只不过就是把结果累加起来了而已。
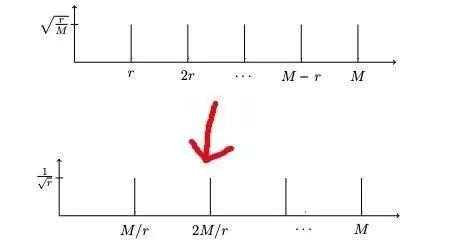
另外值得一提的是,如果f(x)是一个周期为r的函数,那它的QFT也是一个周期函数,周期为M/r,M为采样频率。如下所示:
(图2)
大家可以用DFT的矩阵算式对它进行推导,算是一个课后小作业吧,整个过程我不再赘述。想知道的同学可以在后台留言,我会附上详细推导过程。
通过QFT计算周期
再回过头来看Shor算法。我们知道它的关键点就是求解函数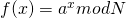
如果是经典计算机的话,那我们就只能一个个数字试从x=1开始,直到发现输出重复为止。而量子计算机的优势就是在于可以一次性把所有的可能都试一遍。所以我们可以对n位量子态|00...0⟩进行QFT,获得所有可能性量子态的叠加:
证明过程如下:
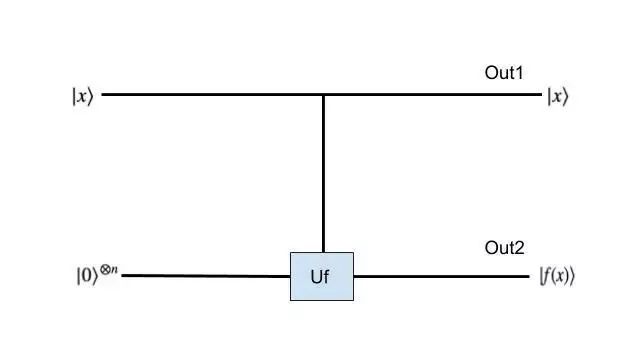
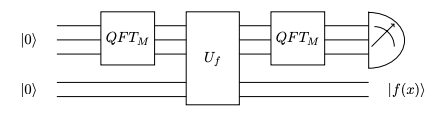
接下来我们可以将上面输出的量子态接入一个2n位的CNOT门电路,其中前半部的n位是作为控制位存储x,而后半部的n位用来存储f(x):
(图3)
所以CNOT的输出就是:
然后我们对CNOT的Out2进行观测。假设探测出来是f(x0),那x只可能是x0,x0+ r,x0+2r,....,x0+kr,其中r就是f(x)的周期。所以Out1就会随即变成:
根据图2的结论,由于f(j) = jr + x0 是一个以r为周期的脉冲函数,所以对Out1再做一个QFT就可以得到一个周期为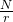
如果我们对QFT输出结果进行观测就会得到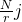
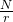
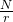
整个算法的过程如下所示:
总结
整篇文章我给大家介绍了运用量子计算机来破解RSA的全过程。整个过程的精髓就在于运用量子的线性叠加性质把所有的可能性在一步以内通通试出来。所以对于比特币来说,理论上它的椭圆曲率加密同样可以通过量子计算机来破解。
但是目前并不需要担心,因为目前为止最先进的量子计算机也就只有20个量子位。而对于160位的椭圆曲率加密,起码需要320个量子位来破译。所以在技术上仍旧有一段距离。但是我相信人类的聪明才智终究会跨越这道鸿沟,到那个时候,比特币就会很危险。这就是为什么我们需要提前布局抗量子加密,以后有机会给大家介绍一些抗量子的加密算法。







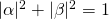
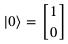
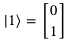
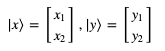
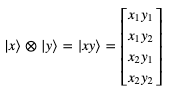
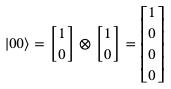
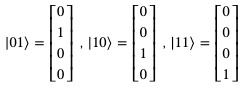
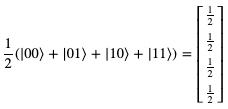
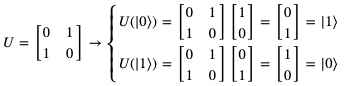

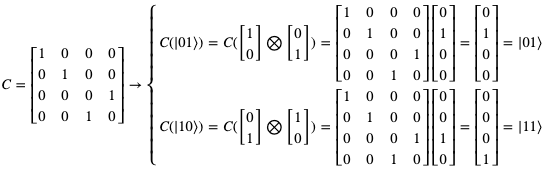
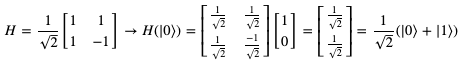
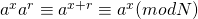
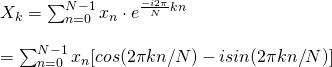
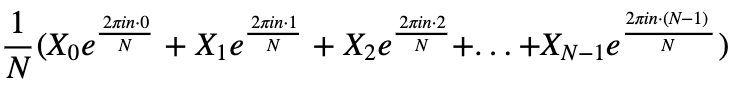
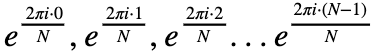
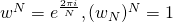
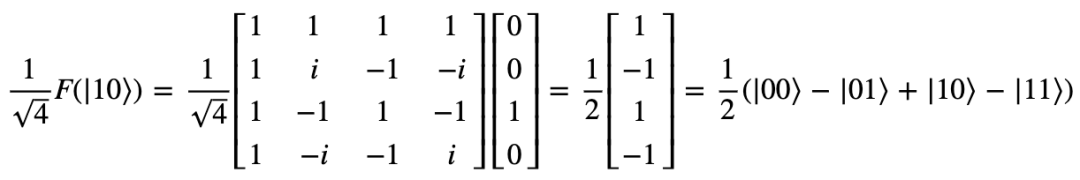
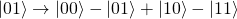
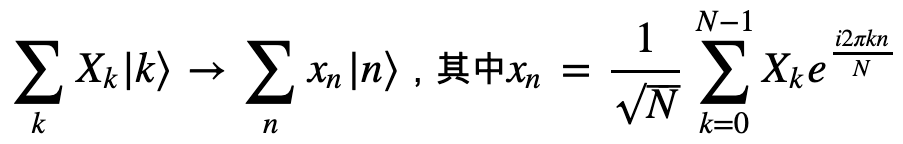
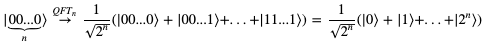
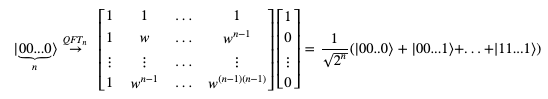
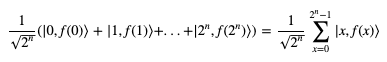
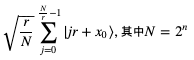
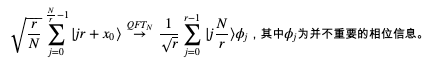

精彩评论